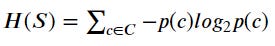Decision-Tree Model Building Metrics Explained in Detail
Learn how to calculate the metrics that were used to building the decision tree model
Learn how to calculate the metrics that were used to building the decision tree model

When you learn your first data science machine learning algorithm, I am sure that Decision Tree is one of the first models you learn. This is by far the simplest yet powerful model, after all.
Why is it famous? I can think of a few reasons; they are:
Easy to use
The learning process is quick.
People could interpret the model (unlike the black box model)
It is the base model for many famous machine learning models.
For those who still do not understand a tree model, let me show you a simple example of the Decision Tree.
Decision Tree
Decision Tree is the based model for every variation within the tree-based algorithm, and the way it works is shown in the image above. Intuitively, it looks like an upside-down tree where the root is on the above, and the leaves are in the bottom part.
The model works by creating a sequence of conditions to reach a result from the data where the decision is taken by going from the sequence upper part (Root) and going down until it reaches the bottom part (leaves). For example, In the image above, when the “Color Green” is True, we going to the “Round Shape” decision node; otherwise, we go to the “Taste Sweet” decision node. Another step was then taken until we reach the bottom part (leaves).
If I make a simpler explanation, a decision tree is an upside-down tree where each node represents variables or features, each decision node or branch represents a decision, and each leaf represents a result or outcome.
The decision tree model is used in both classification and regression problems, which means we could predict both categorical and continuous outcomes, although not both outcomes at the same time.
The next question that came up to mind is, how do we decide which features for each node? How do we decide that this feature is the best?
There are a few algorithm metrics that we can use to build the decision tree, but we would talk about only two of the most famous metrics; Gini Index and Entropy and Information Gain metrics.
The basic idea between these two method metrics is similar. Let me show you an example below.
We have two features X1 and X2, with the colors green and blue is the category you want to predict. We want to find the best feature in the decision tree and their values that split the green and blue categories the best.
But what is the best splitter means? Best splitters could be explained as the features and values that result in the most homogenous (all class categories are similar) results when used for splitting.
How to calculate the homogeneity then? This was when we used the metrics I mentioned before.
Gini Index
Let’s start with the Gini Index. Gini Index is a score that evaluates how good a split is by how mixed the classes are in the split's two groups. Gini index could have a score between values 0 and 1, where 0 is when all observations belong to one class, and 1 is a random distribution of the elements within classes. In this case, we want to have a Gini index score as low as possible.
Gini index equation is expressed in the following image equation.
In the notation above, Pi is the probability of the observation from splitting result for a distinct class (in the example above, green and blue), and n is the number of the class (in our case, is two). By the way, the notation above is a negative-sum symbol, so we subtract instead of addition.
For example, we could try to calculate the Gini index for the X1<2 instances.
The Gini Index for the X1<2 instance is 0.465. Let’s try to calculate for every instance Gini Index.
To find the best splitter by Gini Index, we take the Gini Index weighted average for both instances and choose the lowest Gini Index.
In this case, X1 =2 weighted average Gini index is
((19/29) * 0.465 + (10/29) * 0.18) = 0. 367
and X1= 3 Gini index is
((24/29) * 0.497+ (5/29) *0) = 0.412
We would choose X1 = 2 as the best splitter because it has the least Gini Index.
The steps are repeated until all the nodes have a Gini Index equal to zero (mean only one class found in the leaves), or until it reaches some criteria, we set to stop.
Entropy and Information Gain
What is Entropy and Information Gain metrics? These metrics are two separate metrics that we use to build our decision tree but differ from the Gini Index.
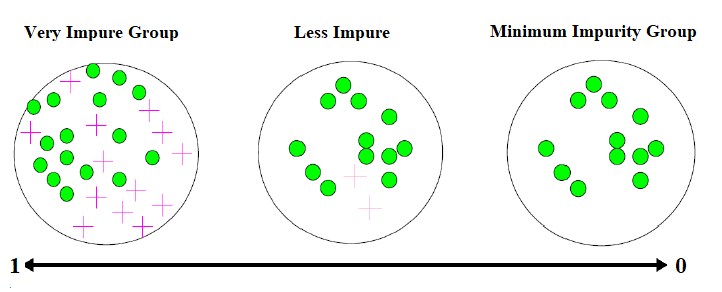
As a starter, Entropy is defined as the measurement of impurity or uncertainty within a dataset. This means that entropy measures the number of class observations mixing within the data. Let me show you by using an image sample below.
When the group is impure (class mixing), the entropy would be close to one, but when the group is pure (only one class within data), the entropy would close to zero.
Entropy could be expressed in the following equation.
Where S is the dataset and p(c) is the probability of each class.
Well, then what is Information Gain? This metric is related to entropy because, by definition Information Gain is a difference of entropy before and after the split by a feature. In other words, Information Gain measure the impurity reduces after splitting.
Information Gain could be expressed in the following equation.
A is the feature used for splitting, T is the whole dataset subset from splitting in feature A, p(t) is the probability of the class in the data subset T, and H(t) is the entropy of the subset.
Information Gain measures the impurity reduces after splitting; it means what we want is the highest Information Gain score because the highest information gain means that the splitting resulted in a more homogenous result.
So, with these metrics, how we calculate which feature gives us the best splitter? There are several steps we need to do, and I would outline each step in detail below.
First, we need to compute the entropy for the data set. Let’s use our previous example dataset (16 green and 13 blue) to calculate our entropy.
After we acquired our dataset entropy, the next step is to measure the Information gain after splitting the feature. In our example above, we have X1 = 2 and X1 = 3 as splitting features. Let’s try to measure Information gain by calculate the entropy subset X1 = 2.
We have acquired both subset entropy, but we still need to sum both of our subset entropy with the subset probability if you remember the previous Information Gain equation. If we put all the number into the Information Gain equation, the Information Gain we have for X1 = 2 is:
With X1 = 2 feature as a splitter, we reduce the impurity by 0.208. Next, we also calculate the Information gain for the X1 = 3 feature. I would show the Information Gain result right now, and what we get for X1 = 3 is 0.168. Because X1 = 2 has the highest information gain, it means we choose the X1 = 2 as our best splitter.
The steps were done until no more separation are possible, or some criteria stopped the calculation we set beforehand (Similar to Gini Index).
Anyway, both the Gini Index and the Entropy and Information gain metrics are the metrics to use in the algorithm to create a decision tree. Both algorithms use a greedy function to find the best features, which means it could take a lot of time, the bigger the dataset.
Conclusion
Decision Tree is one of the most used machine learning models for classification and regression problems. There are several algorithms uses to create the decision tree model, but the renowned methods in decision tree model creation are the ones applying:
Gini Index, or
Entropy and Information Gain
Both these methods measure the impurity of the feature used for splitting but in a different way. Gini Index calculates the binary split impurity result, while Information Gain measures the entropy before and after the splitting result.
I hope it helps!