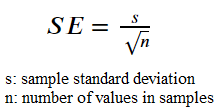Deep Dive Into Error Bar Visualization
Breaking down the fundamental of the error bar
🔥Reading Time: 16 Minutes🔥
Data visualization is a tool for data people to simplify information in a way that humans would understand. The technique lets people quickly catch on to any vital pattern and easily interpret complex data.
Depending on the requirement, data aggregation visualization is sometimes necessary to provide a deeper understanding of the data. For example, we can take average tips between each day and show the result in a bar plot.
In the image above, the error bar is the black line at the top of each bar. However, what is an error bar?
When we visualize the summary statistic, adding an error bar within the graph would be fitting to show the aggregation's uncertainty or spread. Depending on what we measure, it shows how confident we are with the result or how far the values are from the central estimation.
How do we measure the error bar, and what could the error bar tell us about our data? Let's dive further.
Primary Statistic for Error Bar Construction
To understand what the error bars represent, we need to learn some basic statistical terms used to build them. Here are some terms that we need to know.
Descriptive Statistics
Descriptive statistics is a branch that concerns data summarization in an orderly manner to describe the variable relationship in a sample or population. In simpler words, descriptive statistics simplify the process of understanding raw data.
Descriptive statistics use various methods to summarize data, such as summary statistics, graphs, and tables. However, the most popular way to do descriptive statistics is via summary statistics.
The two most commonly used summary statistics are Measures of Central Tendency and Measures of Spread.
Measures of Central Tendency
Measures of central tendency refer to describing the center distribution of our data. These measures provide a singular value that defines the data's central position.
There are three popular measures of central tendency, including:
1. Mean
Mean or average measures central tendency that produces a singular value output representing our data's most common value. However, the mean is not necessarily the value observed in our actual data.
The mean is calculated by summing all the values in our data divided by the number of values. We can represent the mean with the following equation:
For example, we have the following data that shows the number of tips acquired by the restaurant in a day.
Restaurant tips: $1, $2, $4, $2, $3, $5, $10, $3, $6, $7
The mean of the tips can be calculated as follows:
Mean(x̄): (1+2+4+2+3+5+10+3+6+7) / 10 = 4.3
The average of our tips per day is $4.3. As I mentioned, this value does not appear in the actual data but represents the most common value present, as it has the lowest error among all the values in the data.
Additional properties of the mean that might be interesting are that it is a measurement that includes every value in the data set for the calculation and is the only measurement where the sum of the deviations of each observed data point from the mean is always zero.
However, the mean is disadvantageous as it is heavily affected by the outlier, which could skew the summary statistic. As a result, the output might not best represent the actual situation. That is why there is another preferred measurement in skewed cases: the Median.
2. Median
The median iMedianvalue positionedMediane middle of the data, representing the halfway point position of the data (50%). As a measurement of central tendency, the median is preferable when the Medians skewed. Why is that? Let's take a look at the image below.
In the ideal case, the population would follow a normal distribution with identical mean and median values. However, skew often occurs when we sample the data from the population.
When skew occurs, the mean loses credibility as the best central location for the data. On the other hand, the median retains the best positiMedianthe measurement of central tendency, as the outlier or skewed values do not strongly influence it. The example can be seen in the image above.
To calculate the median, we should arrange all Medianlues within our data in ascending order and find the middle value. The median is the middle value forMediand number of data values. However, it is the average of the two middle values for an even number of data values.
For example, if we use the previous data with an even number of data values.
Restaurant tips: $1, $2, $4, $2, $3, $5, $10, $3, $6, $7
We would sort the data in an ascending manner, which results in the following order: 1, 2, 2, 3, 3, 4, 5, 6, 7, 10.
The median is: (3+4)/2 = 3.5
In our data above, we obtain the median as 3.5, the average of Mediano middle values.
We have talked about mean and median, which mainly apply to Mediancal data. However, there is also another type of data: categorical data. Using the mode is more suitable if we want to measure the central tendency of categorical data.
3. Mode
Mode is the value within data with the highest frequency or most occur within the feature. A dataset may have a mode (unimodal), multiple modes (multimodal), or no mode at all (if there are no repeating values).
The mode can be used in numerical or categorical data, but non-numerical data might only use it. This is because if there is no numerical value to calculate, there are no values to measure for both mean and median.
Using the previous data, we can calculate the mode.
Restaurant tips: $1, $2, $4, $2, $3, $5, $10, $3, $6, $7
The mode for the data above would be bimodal, as the most frequent data is $2 and $3.
Measures of Spread
Measures of spread (or variability, dispersion) explain how spread out our data values are. They are often used together with measures of central tendency as they complement the overall data information.
The measures of the spread of information help understand how well our measures of central tendency output. For example, the mean measurement might not fully represent the data if the spread is too large. A higher spread might indicate a significant deviation between the observed data.
The information we have would be different depending on the measure of spread we use. Here are some popular measures of spread to use.
1. Range
The range is the most straightforward measure of spread, as the output is the difference between the largest (Max) and the smallest value (Min) in the data.
Range = Maximum value — Minimum Value
If we use our previous data to calculate the range.
Restaurant tips: $1, $2, $4, $2, $3, $5, $10, $3, $6, $7
The maximum value is 10, and the minimum value is 1. The range would be 10–1, which is 9. It is as simple as that.
The information from range measurement might be limited, but it is helpful if we have a certain assumed threshold for our data. For example, we observed the school children's age, and the range is 5 to 100 years old — which means we have an error in the data.
2. Variance
Variance measures how our data spread based on the data mean. It is calculated by squaring the differences of each value to the mean divided by the number of values. We subtract the number of values by one because we usually only work with the data samples. The equation for sample variance is shown in the following image.
The subtraction is present as sample data contain uncertainty compare to the data population. If you are sure you are working with the population data, you don't need the subtraction.
With the previous data sample, we can calculate the variance.
Restaurant tips: $1, $2, $4, $2, $3, $5, $10, $3, $6, $7
The variance of the above data is 7.57.
What is the variance interpretation? The variance score indicates how far the data is spread between the mean and each other. The higher the score, the wider the data is spread.
However, variance is also sensitive to the outlier. As we squared the scores' deviations from the mean, we gave more weight to the outlier. The variance score then may not correctly represent the data.
3. Standard Deviation
Standard deviation is the most used way to measure data spread. We can calculate it by taking the variance's square root, as shown in the following equation.
What is the difference between Variance and Standard Deviation?
The variance value only indicates how far our values were from the mean. As the variance equation uses the value squaring method, the variance unit differs from the original value. That is why the variance value often only serves as an indicator.
In contrast, the standard deviation value is the same unit as the original data value. This means that the standard deviation value can be used directly to measure the spread of our data.
The most common application for standard deviation to measure the data spread is using the empirical rule or 68–95–99.7 rule to estimate the data interval. Let's take a look at the image below.
The chart above shows a "68% data (±1 STD) sign". This indicates that if the data follows a normal distribution, approximately 68% of the data points are estimated to fall within one standard deviation of the mean. For 2 and 3 standard deviations, it's estimated that roughly 95% and 99.7% of the data fall within those ranges, respectively.
Let's use the previous data sample to calculate the standard deviation.
Restaurant tips: $1, $2, $4, $2, $3, $5, $10, $3, $6, $7
If we take the square root of the variance, the standard deviation is around 2.75.
With the empirical rule, 68% of the data would be roughly 4.3 ± 2.75 (2.05 to 7.55).
A weakness of the standard deviation is its sensitivity to outliers, as its calculation depends on the mean. If we realize that the outlier might affect the result, we can use another method that is less sensitive to the outlier — Interquartile Range.
4. Interquartile Range
Interquartile Range or IQR is a measure of spread with the output of the differences between the first and third quartile data. The quartile itself is a value that divides the data into four different parts. Let's take a look at the following image to understand it better.
The quartile is not the result of the division but, instead, the values that divide the data. There are three kinds of quartiles — Q1, Q2, and Q3. Each quartile represents value in their respective position in the data. For example, Q2 is the data median.
For Q1 and Q3, it's the middle value of both the lower and upper datasets when divided by the median. Q1 is the middle betweMedian minimum value in the data and the median, while Q3 is between thMedianmum value and the median.
Using the previous datMediancan calculate the IQR.
Restaurant tips: $1, $2, $4, $2, $3, $5, $10, $3, $6, $7
The Q1 for the above data would be 2, and Q3 would be 6. This means the IQR would be 6–2, which is 4.
Inferential Statistics
While descriptive statistics provide information about the data sample, inferential statistics generalize the population based on that sample.
For example, we want to understand how Indonesians perceive data science. However, the study would take too much time if we surveyed every single person in the Indonesian population. We use the sample data to represent and make inferences about the Indonesian population.
Many techniques fall under inferential statistics, including hypothesis testing (t-test, ANOVA, etc.). However, we will only discuss the inferential statistic relevant to the error bar.
1. Standard Error
The standard error is a measurement in inferential statistics to estimate how likely a given sample statistic represents the true parameter of the population. The standard error aims to inform how the statistic sample would vary if we repeat the experiment with data samples from the same population.
Standard error is important in our data analysis because it helps us measure how well our sample data represents the true population and ensures that we are confident with our data sampling.
There are many types of standard error, but the standard error of the mean (SEM) is the most commonly used. SEM would inform us how well the mean would represent the population given the sample data. To calculate SEM, we would use the following equation.
The higher the sample size, the smaller the standard error. Smaller standard errors show that our sample is more likely to represent the population.
Let's calculate the SEM using our previous sample data.
Restaurant tips: $1, $2, $4, $2, $3, $5, $10, $3, $6, $7
The standard deviation of our data is 2.75. If we put it into the standard error equation, the output is around 0.87.
SEM is often reported with the mean. The restaurant tips mean with the standard error is 4.3 ± 0.87(SEM). This shows that the population mean is estimated to fall around 3.43–5.17.
The standard error is good for estimating the true population parameters, but there is a better way to estimate the population parameter confidently. The best way to report a standard error is to use the confidence interval.
2. Confidence interval
Confidence interval information is similar to the standard error — to estimate the true population parameter. However, the confidence interval introduces the confidence level. With confidence level, we can estimate the range of true population parameters with a certain confidence percentage.
Confidence in the statistic can be described as a probability. For example, a confidence interval with a 95% confidence level means that 95 out of 100 times the true mean population estimate would be within the confidence interval upper and lower values.
To understand the concept better, let's look at the equation for mean confidence intervals.
In the equation above, we can see familiar parameters such as the mean and the standard error. But what about the Z parameter? The equation for the confidence interval above requires the z-score, which is the critical value when we follow the z-distribution. We also called the z-score times standard error the Margin of Error.
The z-score is acquired by defining our intended confidence level (e.g., 95%) and then referencing the z-critical value table to determine the z-score (1.96 for a confidence level of 95%). Additionally, if our sample is small or below 30, it is advised to use the t-distribution table.
Let's calculate the confidence interval with the previous data sample.
Restaurant tips: $1, $2, $4, $2, $3, $5, $10, $3, $6, $7
The data mean is 4.3, and the standard error is 0.87. With a confidence level of 95%, we input all the values into the confidence interval equation. The result is 4.3 ± 1.71.
The interpretation of the above result is that our restaurant tips' actual mean population is between 2.59 and 6.01, with a 95% confidence level.
Exploring Error Bar
We have learned a lot about basic statistical knowledge, but how is it beneficial to understand the error bar? First, let's break down what error bar functions are in the graph.
An error bar is useful in conjunction with another chart to provide information about the measurement spread or uncertainty. While the numerical data might provide the same information, an error bar provides a visual representation that can help the audience understand better.
For example, I have the restaurant tip data in the table below.
The data above is easy to understand, but representing the data visually would provide more clarity. Let's bring the data into chart visualization.