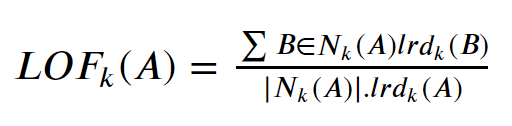Novelty Detection with Local Outlier Factor

Detecting whether a new data is an outlier or not

Detecting whether a new data is an outlier or not

Photo by Randy Fath on Unsplash

Novelty detection might be a more rare term to be heard by some people compared to outlier detection. If outlier detection aims to find the anomaly or significantly different data in a dataset, novelty detection aims to determine new or unknown data to be an outlier or not.

Novelty detection is a semi-supervised analysis because we would train training data that was not polluted by outliers, and we are interested in detecting whether a new observation is an outlier by using the trained model. In this context, an outlier is also called a novelty.

In this article, I would explain how to perform a novelty detection using the Local Outlier Factor (LOF). Let’s just get into it. Although, in case you want to skip all the theory and just want to get dirty with the coding part, just skip this next section.

Local Outlier Factor (LOF)

Local Outlier Factor or LOF is an algorithm proposed by Breunig et al. (2000). The concept is simple; the algorithm tries to find anomalous data points by measuring the local deviation of a given data point with respect to its neighbors. In this algorithm, LOF would yield a score that tells if our data is an outlier or not.

LOF(k) ~ 1 means Similar density as neighbors.

LOF(k) < 1 means Higher density than neighbors (Inlier/not an outlier).

LOF(k) > 1 means Lower density than neighbors (Outlier)

In the above equation, I have introduced you to a k parameter. In the LOF algorithm, the locality is given by k-nearest neighbors, whose distance is used to estimate the local density. The distance would then be used to measure the local deviation and pinpoint the anomaly.

k parameter is a parameter we set up to acquire a k-distance. The k-distance is the distance of a point to its kth neighbor. If k were 4, the k-distance would be the distance of a point to the fourth closest point. The distance itself is the metric of distance computation that we could choose. Often it is ‘Euclidean,’ but you could select other distances.

k = 4 with the point reach the fourth closest point (Images created by Author)

In case you are wondering, every data point in our dataset would be measured for the k-distance in order to measure the next step.

The distance is now used to define what we called reachability distance. This distance measure is either the maximum of the distance of two points or the k-distance of the second point. Formally, reachability distance is measured below.

reachability-distance k(A,B)=max{k-distance(B), d(A,B)}

Where A and B are the data point, and reachability distance between A and B is either the maximum of k-distance B or distance between A and B. if point A is within the k-neighbors of point B, then the reachability-distance k(A, B) will be the k-distance of B. Otherwise, it will be the distance between A and B.

Next, we would measure the local reachability density (lrd) by using the reachability distance. The equation to measured lrd is estimated as below.

lrd(A) = 1/(sum(reacheable-distance(A,i))/k)

Where i is the neighbors of point A (Point where A can be “reached” from its neighbors), to get the lrd for point A, we calculate the sum of the reachability distance A to all its k-nearest neighbors and take an average it. The lrd is then is the inverse of the average. LOF concept is all about densities and, therefore, if the distance to the next neighbors is longer, the particular point is located in the sparser area. Hence, the less dense — the inverse.

Here, the lrd tells how far the point has to travel to reach the next point or cluster of points. The lower the lrd means that the longer the point has to go, and the less dense the group is.

The lrd of the center point is the average reachability distance to its nearest neighbors, which are points in lower left except for the (1,1) point. However, these neighbors have other lrds as their nearest neighbors don’t include the center point. (Images created by Author)

The local reachability densities then compared to the other neighbors with the following equation.

The lrd of each point is compared to the lrd of their k-neighbors. The LOF would be the average ratio of the lrds of the neighbors of A to the lrd of A. If the ratio is greater than 1, the density of point A is smaller than the density of its neighbors. It means, from point A, it needs to travel much longer distances to get to the next point or cluster of points than from A’s neighbors to their next neighbors.

The LOF tells the density of the point compared to the density of its neighbors. If the density of a point is smaller than the densities of its neighbors (LOF >1), then it is considered as an outlier because the point is further than the dense area.

LOF algorithm advantages are that it can perform well even in datasets where abnormal samples have different underlying densities. This is because LOF is not how isolated the sample is, but how isolated it the sample compared to the surrounding neighborhood.

Novelty Detection via LOF

We would use the LOF provided by scikit-learn to help us train our model.

#Importing the module

import pandas as pdimport seaborn as snsfrom sklearn.neighbors import LocalOutlierFactor

#Importing the dataset. Here I use the mpg dataset as an examplempg = sns.load_dataset('mpg')

For the introduction, let’s try using LOF as an Outlier Detection model before using the model for Novelty Detection.

#Setting up the model. K is set by passing the n_neighbors parameter with integer. 20 is often considered good already to detect an outlier. By default the distance metric is Euclidean distance.

lof = LocalOutlierFactor(n_neighbors = 20)

#Training the model, I drop few columns that was not a continuous variable

mpg['lof'] = lof.fit_predict(mpg.drop(['cylinders', 'model_year', 'origin', 'name'], axis = 1))

#Getting the negative LOF score

mpg['negative_outlier_factor'] = lof.negative_outlier_factor_

mpg

Below is the result, where we get the LOF classification and negative LOF score. If lof equal to 1, then it is considered as an inlier; if it is -1, then it is an outlier. Let’s try to get all the outlier data.

mpg[mpg['lof'] == -1]

The contamination or outlier depends on the LOF score. By default, if the score of the negative_outlier_score is less than -1.5, it would be considered as the outlier.

Now, let’s try to use the model for Novelty Detection. We need to train the model once more because there is an additional parameter we need to pass on.

#For novelty detection, we need to pass novelty parameter as True

lof = LocalOutlierFactor(n_neighbors = 20, novelty = True)lof.fit(mpg.drop(['cylinders', 'model_year', 'origin', 'name'], axis = 1))

We only train the model, and we would not use the training data at all to predict the data. Here we would try to predict the new unseen data.

#Predict a new random unseen data, the dimension must match the training data

lof.predict(np.array([109, 310, 190, 3411, 15]).reshape(1,-1))

Out: array([1])

The output would be either 1 or -1, depends if it is an outlier or not. If you want to get the negative LOF score, we could also do it with the following code.

lof.score_samples(np.array([109, 310, 190, 3411, 15]).reshape(1,-1))

Out: array([-1.34887042])

The output would be the score in the form of an array. And that is it, I have shown you how to do a simple novelty detection with LOF.

Conclusion

Novelty Detection is an activity to detect whether the new unseen data is an outlier or not. Local Outlier Factor is an algorithm used for Outlier Detection and Novelty Detection. It depends on the k parameter we pass on. Often k = 20 is working in general, but if you feel the data have a higher number of outliers, you could increase the number.

I hope it helps.