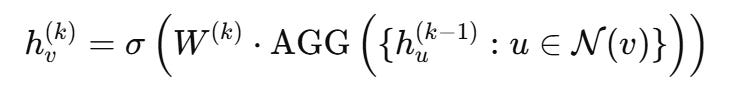What Is Graph Machine Learning and Why It Matters
Few things you should know when working on the graph
If you're ever working with traditional machine learning models, most assume that data points are independent and identically distributed. Although this assumption works well for images, text, and tabular datasets, it fails to account for scenarios where relationships between data points are as meaningful as the data points themselves.
This is where Graph Machine Learning (Graph ML) comes into play. Instead of analyzing each observation separately, Graph ML models work directly on graph-structured data that consists of networks of nodes (entities) and edges (relationships).
This structure enables them to naturally represent and learn from the interconnectedness of many real-world systems, such as social networks, transportation systems, protein interaction maps, and knowledge graphs.
By leveraging the attributes of individual nodes and the topology of their connections, Graph ML enables tasks such as predicting missing links, classifying nodes or entire graphs, and uncovering hidden patterns in complex systems.
In this article, we will explore the Graph ML concept further, which is perfect if you are unfamiliar with it.
Let’s get into it.
Graph Basics
At its core, a graph is a data structure that models relationships. It is defined as G=(V,E), where:
V is the set of nodes (or vertices), each representing an entity.
E is the set of edges representing a connection between two nodes.
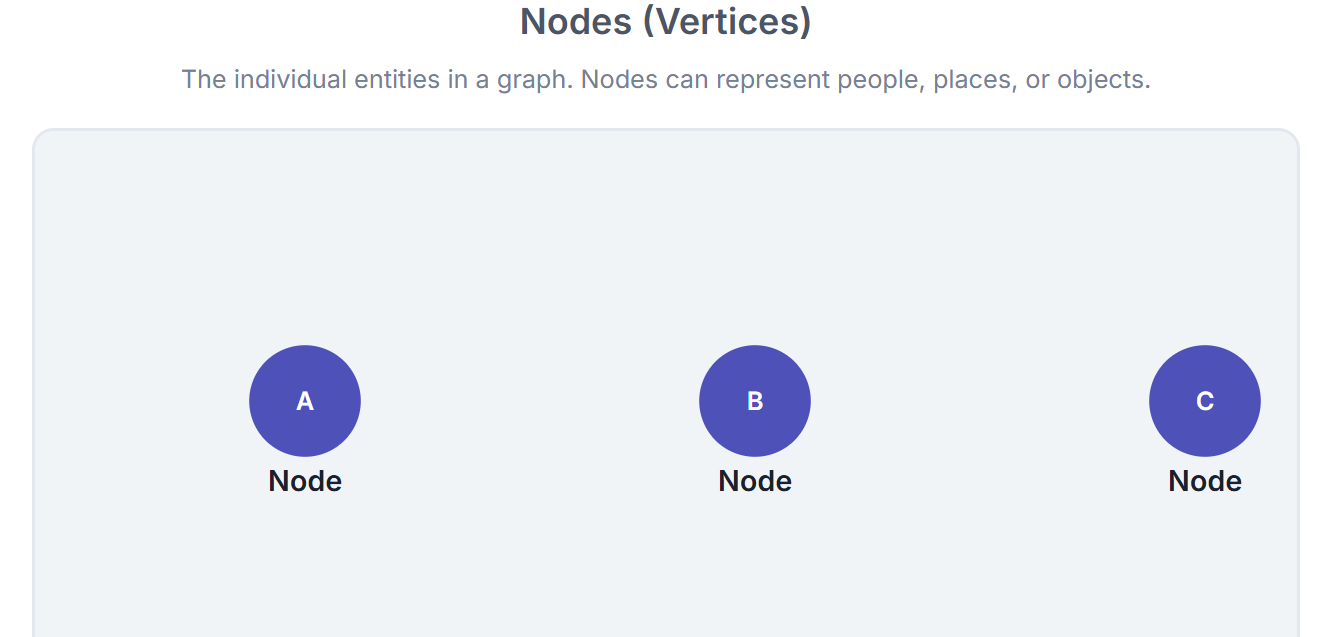
1. Nodes (Vertices)
Nodes are the fundamental units of a graph. In real-world examples:
In a social network, each node could represent a user.
In a transportation network, each node could be a city or station.
In a molecular graph, each node might be an atom.
Nodes can have attributes that are either structured or unstructured features describing them. These attributes can include numerical values (e.g., age, temperature) or categorical data (e.g., molecule type).
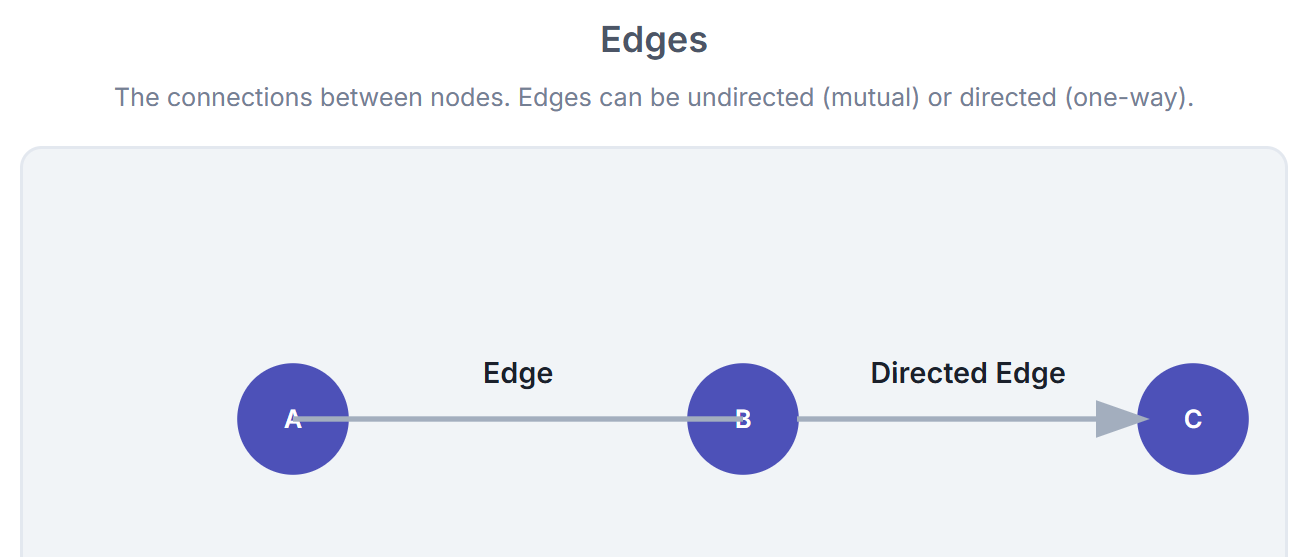
2. Edges
Edges define the relationships between nodes. They come in several types:
Directed edges: Show one-way relationships (e.g., Twitter “follows”).
Undirected edges: Show mutual relationships (e.g., Facebook friendships).
Weighted edges: Show a value indicating the strength, cost, or capacity of a connection (e.g., distance between cities, similarity score between items).
Edges can also possess their own attributes, which are often vital for prediction tasks, such as timestamps in temporal graphs or bond types in chemical compounds.
3. Graph Types
Depending on their complexity and purpose, graphs can be:
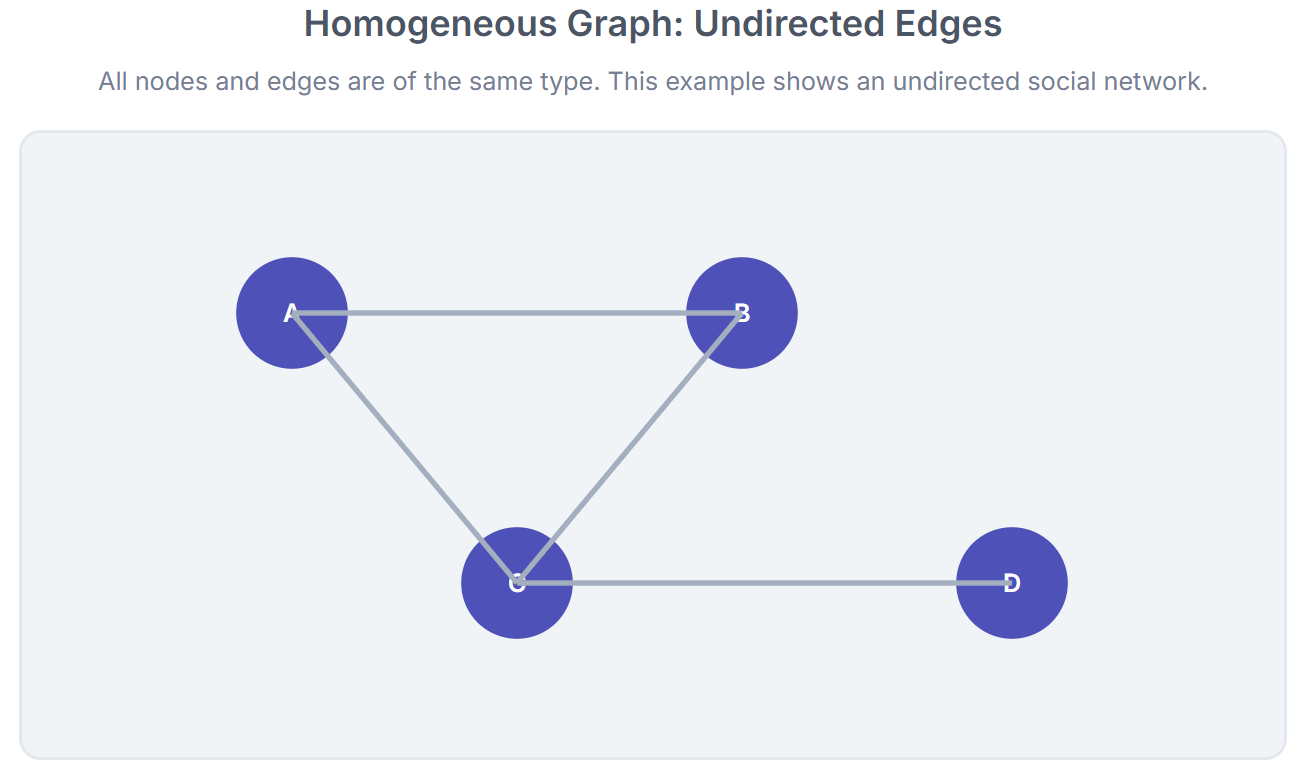
Homogeneous graphs: All nodes and edges are of the same type (e.g., a network of people connected by friendships).
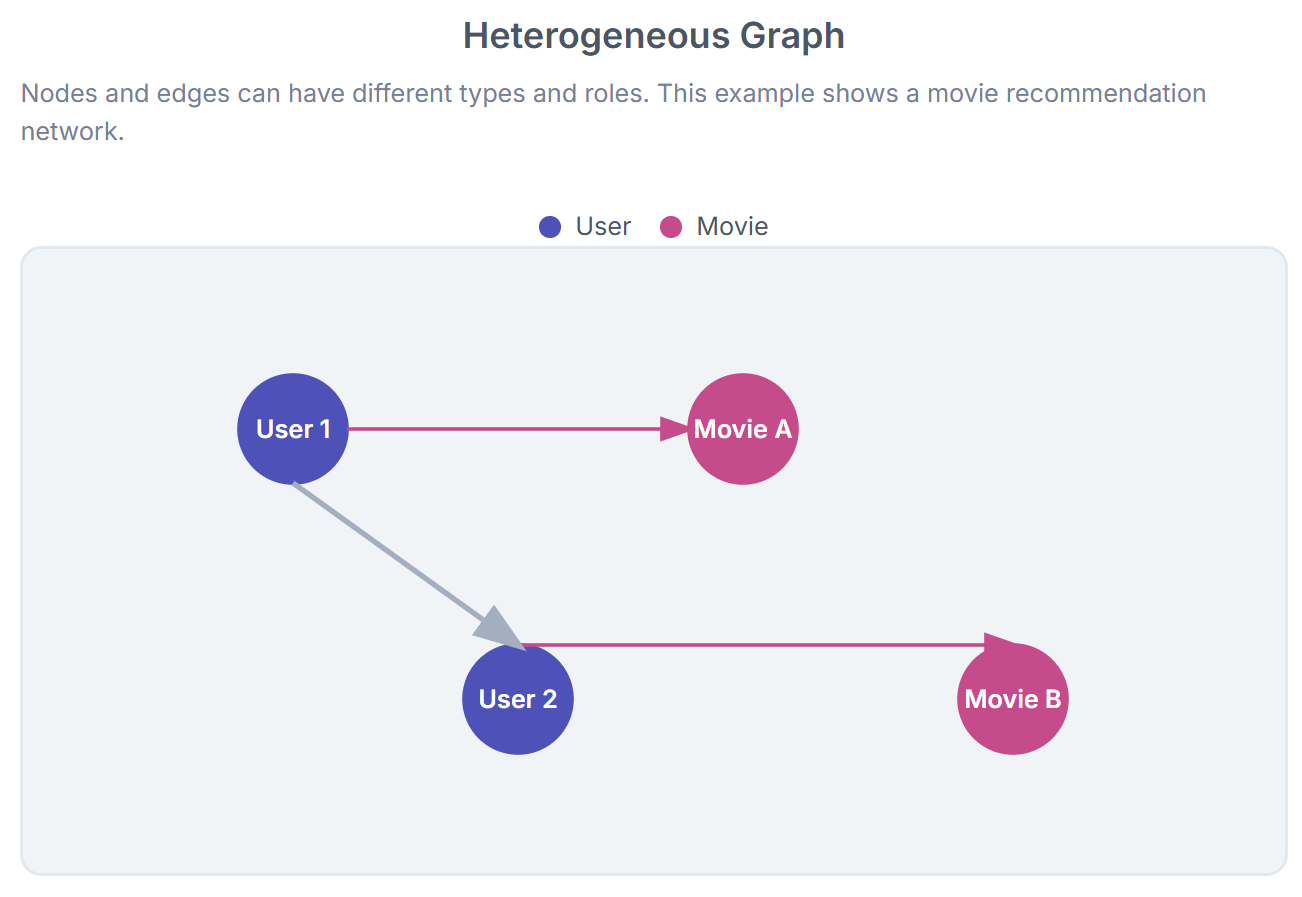
Heterogeneous graphs: Multiple node and edge types coexist, often with different attributes (e.g., a movie recommendation graph linking users, movies, genres, and ratings).
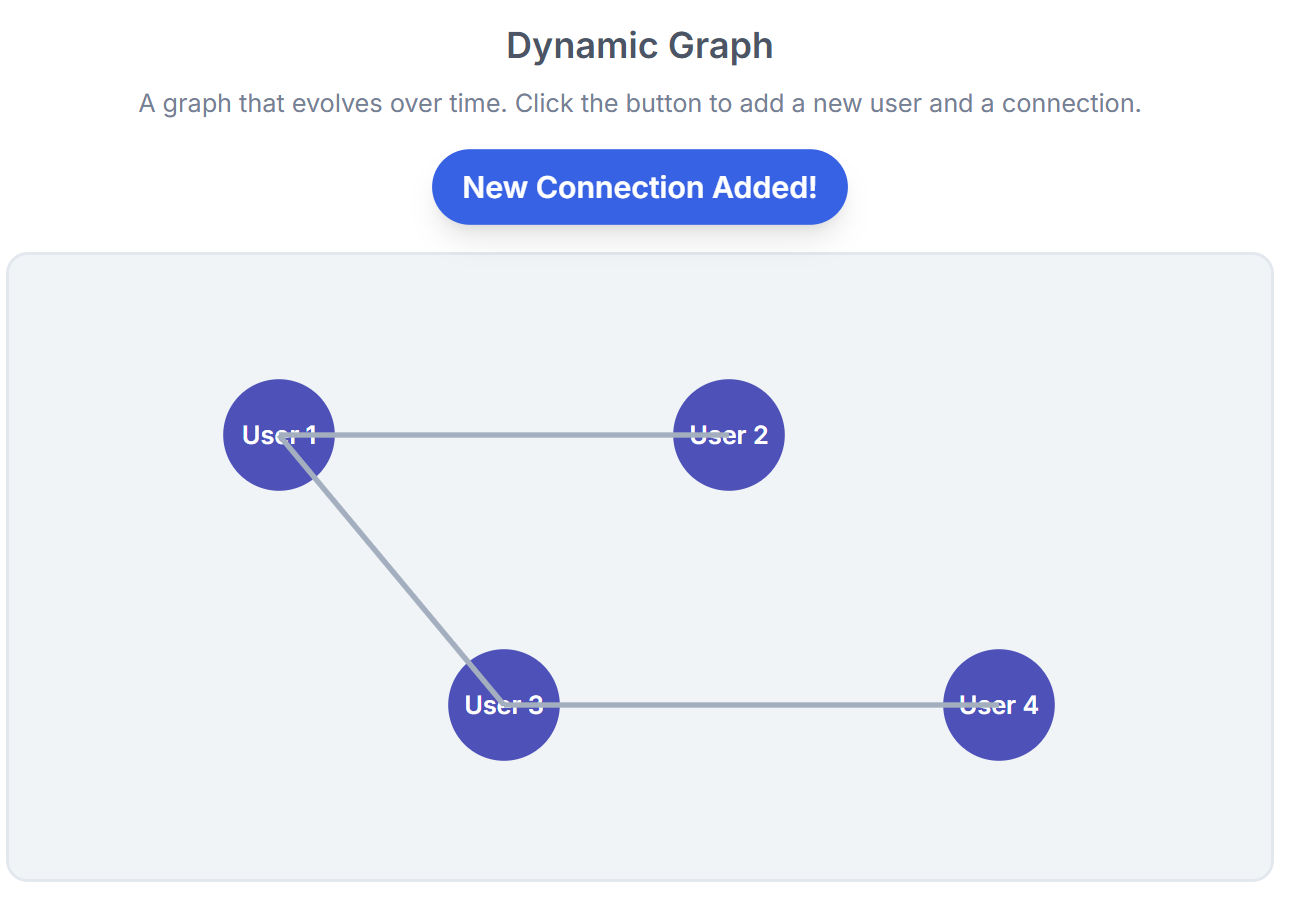
Dynamic graphs: Graphs that change over time, with new nodes and edges appearing or disappearing (e.g., real-time financial transaction networks).
4. Local vs. Global Structure
One of the main benefits of graphs is their ability to represent both:
Local relationships: the immediate neighbors of a node.
Global structure: how a node integrates into the overall network topology.
For example, in a knowledge graph, local relationships might show you that “Node A is connected to Node B.” However, the overall structure could reveal that both nodes are part of the same densely connected community, indicating a deeper connection.
This rich relational structure is precisely what Graph Machine Learning models aim to utilize. Unlike tabular or image data, where relationships are often static, graphs make those relationships clear, allowing algorithms to use them directly for prediction and pattern detection.
How Graph Machine Learning Works
At the core of modern Graph Machine Learning is that nodes are interconnected; their meaning often depends on their connections. The main challenge is creating algorithms to learn from node/edge features and the graph structure.
Today's primary method involves Graph Neural Networks (GNNs), which expand neural networks to process graph-structured data. The core idea is called the message passing paradigm.
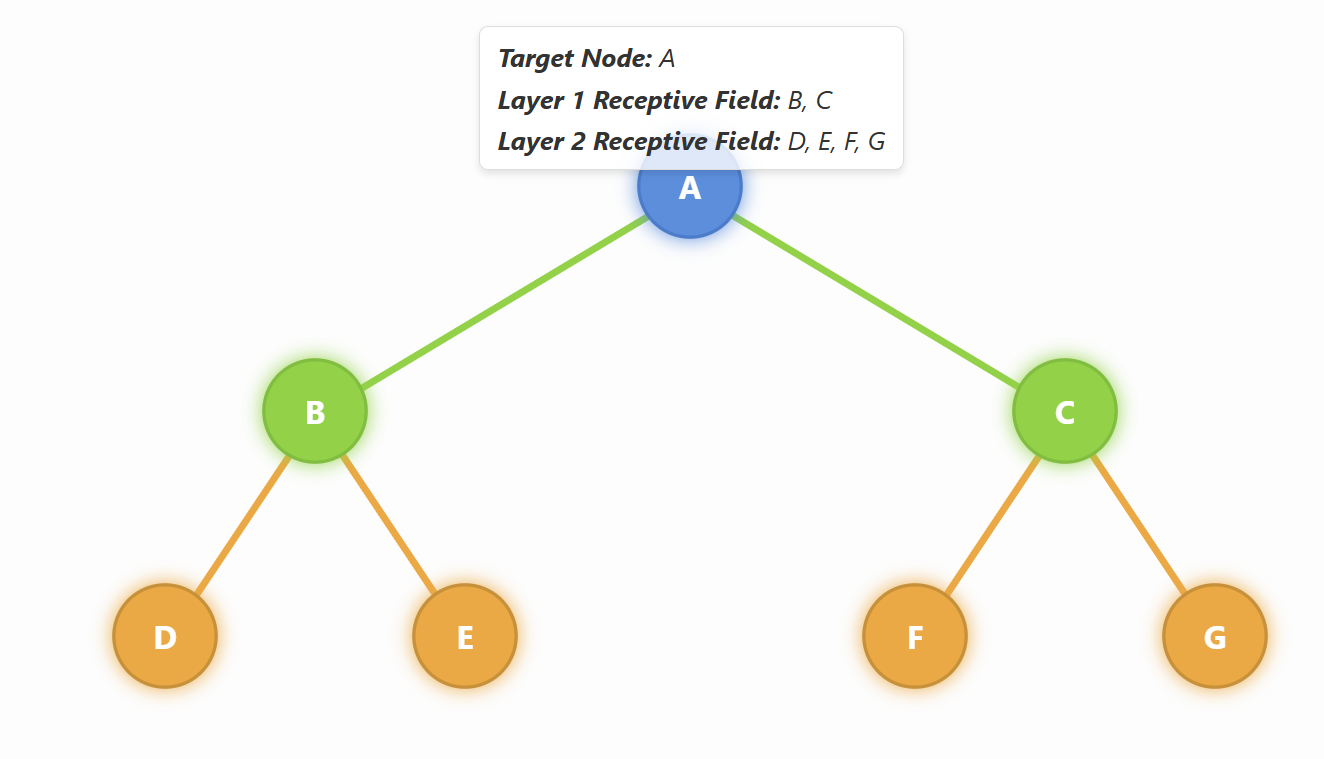
1. The Message Passing Paradigm
In message passing, each node updates its representation by gathering information from its neighbors. This occurs in multiple steps or layers, with each layer increasing the node's "receptive field."
Think of it like this:
Layer 1: A node learns from its immediate neighbors.
Layer 2: The node learns from neighbors of neighbors.
Layer k: The node gathers information from all nodes within k hops in the graph.
The process involves three main stages for each layer:
Message generation: Each neighbor sends information based on its current features.
Aggregation: The node combines messages from all its neighbors, often using operations like sum, mean, or max pooling.
Update: The node updates its feature vector through a learnable transformation (such as a linear layer followed by a non-linear activation).
Formally, a single GNN layer can be expressed as:
Where:
2. Node Embeddings
The goal of message passing is to produce node embeddings, which are low-dimensional, information-rich vectors that encode both a node’s attributes and its structural position in the graph.
Node embeddings are numerical vector representations that encode both:
Node attributes: the inherent features of a node (e.g., age, role, molecular type).
Structural context: how the node is positioned in the broader network (e.g., which communities it belongs to, how central it is, what kinds of neighbors it has).
Because embeddings combine feature information and graph topology, they are much more informative than features alone.
Once we have these embeddings, they become a universal representation of nodes that can be fed into standard machine learning models.
This means a Graph ML model can recognize patterns like “nodes with certain attributes and specific neighbor structures tend to behave similarly,” even if those patterns are too subtle for traditional models to detect.
Graph Machine Learning Application and Outlook
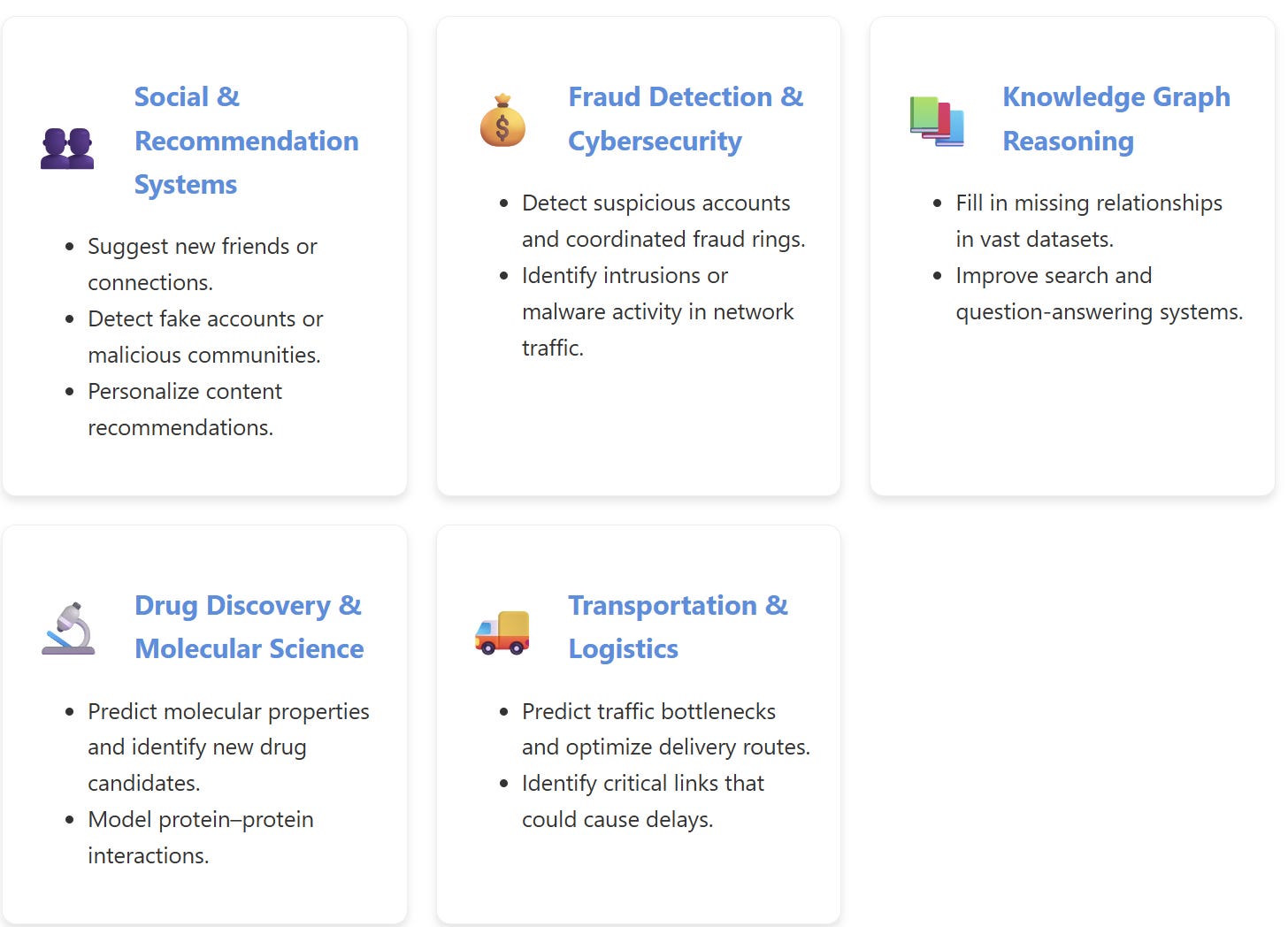
Graph Machine Learning has transformed multiple industries by allowing AI systems to reason about relationships, context, and network structure. Here are a few applications you can expect:
While Graph Machine Learning has demonstrated impressive results, several challenges still exist.
Scalability: Large graphs with millions of nodes and edges need efficient algorithms and sampling techniques.
Dynamic Graphs: Many real-world graphs evolve over time; modeling this temporal aspect remains an active research area.
Interpretability: Understanding why a GNN made a specific prediction is still challenging, which is essential in sensitive fields like healthcare and finance.
Multimodal Integration: Merging graph data with text, images, and other modalities can enable more comprehensive and powerful AI systems.
Graph ML is rapidly moving from research to practical applications. As algorithms advance and computing power grows, we can expect graph-based reasoning to become a key component of AI systems, not only in obvious areas like social networks but also in any domain where relationships matter.
Book Recommendation
For additional practical and production-ready learning material, Graph Machine Learning (2nd Ed.) by Aldo Marzullo, Claudio Stamile, and Enrico Deusebio is an essential read for anyone wanting to work with connected data.
This book contains real-world Graph ML use cases, from GNNs to RAG with LLMs, which you don’t want to miss.
👉Grab the book here.
Love this article? Comment and share them with Your Network!
If you're at a pivotal point in your career or sitting on skills you're unsure how to use, I offer 1:1 mentorship.
It's personal, flexible, and built around you.
For long-term mentorship, visit me here (you can even enjoy a 7-day free trial).