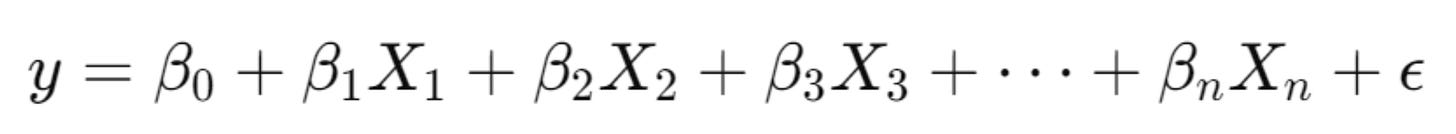Why is Confidence Interval Important in Interpreting Regression Coefficient? - NBD Lite #27
The importance of uncertainty estimation
The regression model is popular and has been standard in many businesses, especially in the financial industry.
It’s become the “standard” because of how easy it is to develop and how interpretable they are.
The interpretability comes from the Regression Coefficient.
However, there is another concept called Confidence Interval (CI) that you acquire when developing the model.
So, why is CI important in the Regression Coefficient interpretation?
Let’s explore it together! Here is the summary of what we would talk about.
Regression Coefficient
When discussing the Regression Model, we often refer to the generalized linear model (GLM), especially the linear regression model.
The equation is simple, as shown in the image below.
The β1,β2,…,βn are the coefficients, where each represents how much the dependent variable (y) changes when the related independent variable (x) increases by one unit, while all other variables remain constant.
For example, we have a coefficient like the one below, where we develop a linear regression model to predict house prices.
Increasing one unit in the bedroom would increase the prediction value equal to 15172.85.
In contrast, increasing one unit in the Garage would decrease the prediction value equal to 4677.36.
However, the coefficient itself is an estimate based on sample data.
The number could vary if you were trying to collect a new sample.
This is why confidence intervals are so important for trusting the coefficient.
Confidence Interval for Regression Coefficient
A confidence interval (CI) is a range of values that provide an estimate of uncertainty from statistical measures.
Coming from the sample, CI provides an estimate of the true population parameter. This means that the true coefficient in the population is within the range with a certain level of confidence.
For example, if the confidence interval for a coefficient is [120, 180], it means that with 95% confidence, the true coefficient is between 120 and 180.
Usually, Coefficient Intervals can be visualized with the error bar like below.
Whenever you calculate the Regression Model coefficient, it usually comes with the Confidence Interval as well.
import statsmodels.api as sm
X = sm.add_constant(X) # Add a constant for intercept
model = sm.OLS(y, X).fit()
print(model.conf_int())So, why is it useful to understand the Confidence Interval for Regression Coefficient? There are various reasons, including:
As mentioned previously, the Confidence Interval provides a precise estimate of the true value of the coefficient in the population. It gives the user more confidence about the interpretation we get from the coefficient.
Confidence intervals help determine if the feature is statistically significant. If the interval includes zero, this suggests that the predictor might not have any effect at all, and the interpretation might not be useful at all.
Lastly, the Confidence Interval could help in Decision-Making as it provides a range of possible interpretations for real-world applications. For example. Having Confidence Intervals anywhere from $120 to $180 per unit increase can help in the pricing strategies.
That’s all you need to know why Confidence Interval is important for Regression Coefficient.
Are there any more things you would love to discuss? Let’s talk about it together!
👇👇👇