Why K-Means Failed at Non-Convex Shape Data-NBD Lite #8
Why K-Means Failed at Non-Convex Shape Data-NBD Lite #8
The popular clustering methods "might" not a silver bullet for everything.
K-Means is a popular clustering algorithm that separates datasets into K number of non-overlapping clusters.
It’s widely used in data analysis and mining, and it’s very intuitive.
However, K-Means has a few weaknesses. One of them is that it failed at the Non-Convex shape data.
Let’s take a look at the following clustering visualization.
When the dataset is in a convex or roughly spherical shape, K-Means easily clustered them.
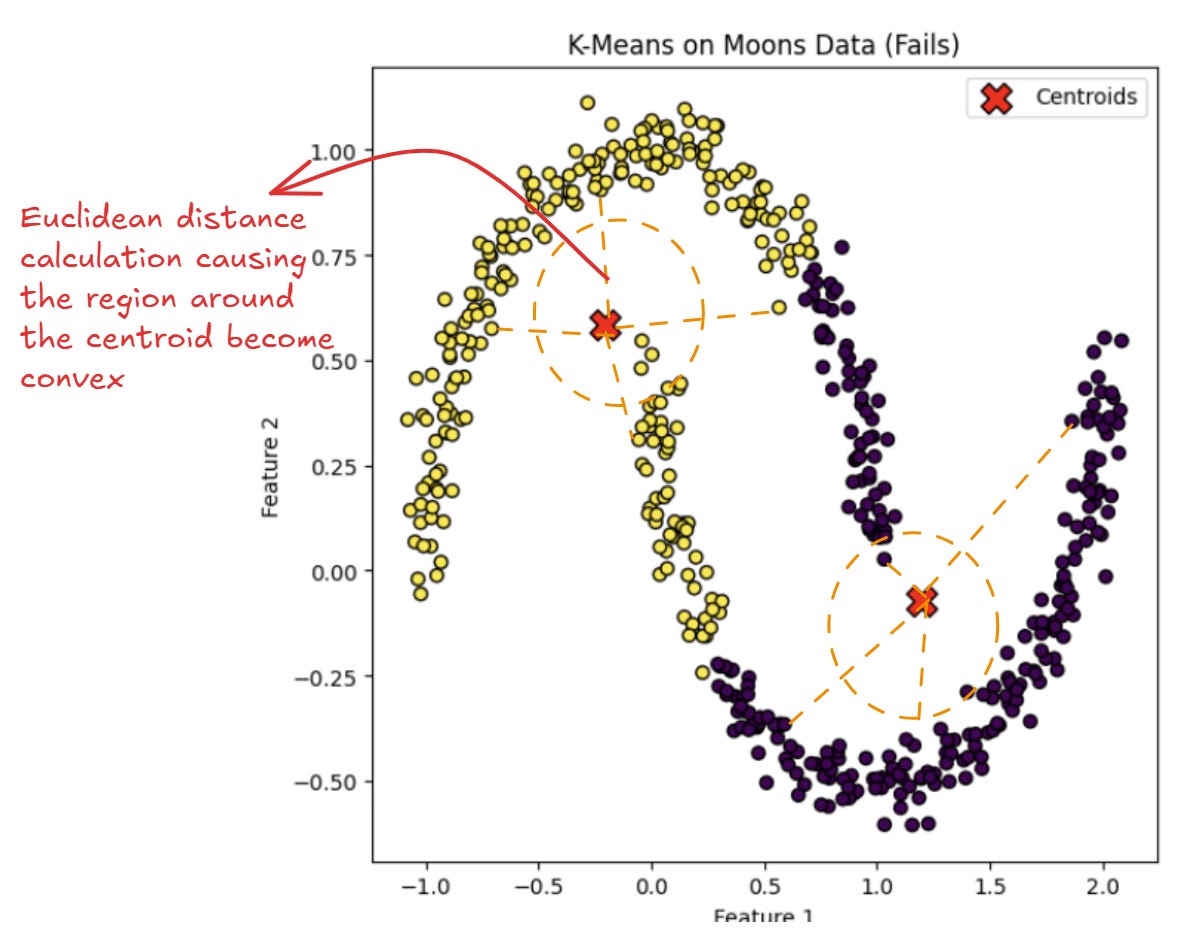
However, let’s look at the K-Means process when the dataset is in the crescent moon shape.
We can see that the K-Means can’t be separated enough; instead, they mix up data points from different curves.
Humans can easily see how data on the moon should be separated. However, machine algorithms only have the information from their algorithm.
So, let’s understand a little bit about how K-Means works. Here is a simple visualization of how the algorithm performs its clustering process.
K-Means basically works by setting the K number of clusters we want, and we initiate the centroid as much as the K.
We would then assign each data point to the centroid based on the closest Euclidean distance.
By iterating the process to reposition the centroid until it converges, we would get the clustering result.
As we see the method, the assumption is that K-Means would inherently assume that the clusters are convex in shape.
The assumption comes from the algorithm dependence of Euclidean Distance.
With Euclidean distance, each cluster is basically a convex set because any two points within a cluster are connected by straight lines that lie entirely within that cluster.
The convex set property is present because data points are assigned to the nearest centroid and the regions where each centroid is the closest form convex shapes.
Because no lines exit the cluster between two data points, the K-Means would inherently produce convex clusters.
As a result of the convex property, the algorithm has a hard time capturing clusters where the line between two points might pass outside the cluster boundaries.
If you evaluate the dataset as in non-convex shape, you might want to try other clustering alternatives such as:
That’s all for today! I hope this helps you understand why K-Means might not be the best for non-convex shape data.
Are there any more things you would love to discuss? Let’s talk about it together!
👇👇👇
FREE Learning Material for you❤️
👉Unsupervised Learning by Zoubin Ghahramani