NBD Lite #4: Effect of Min Samples Leaf on Tree Model Complexity

How you can manipulate the parameter for your work

The tree-based model is a popular classification algorithm in many business use cases.

As I have mentioned in the previous post, the tree-based model, such as a decision tree, can handle non-linear datasets thanks to its algorithm.

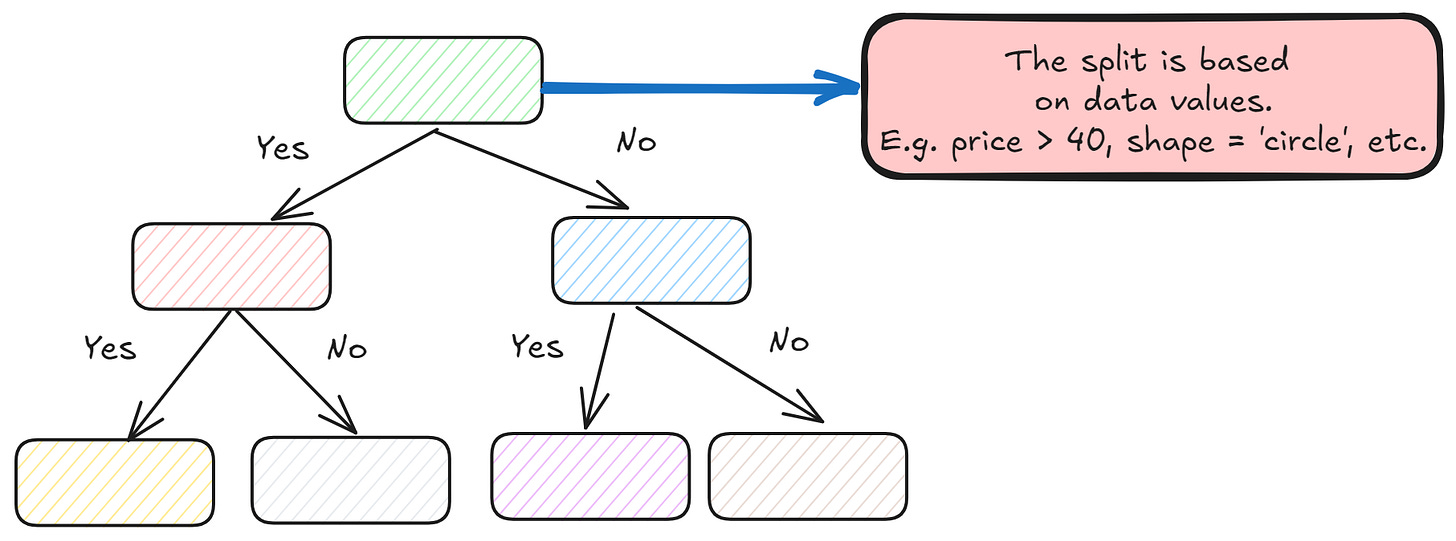
The non-linearity came from the flowchart-like structure to split the data based on the data.

The split premise is based on the data values identified from the node-splitting function, such as Gini Impurity or Entropy.

In a usual decision tree, the terminal node (leaf) represents the final decision, where the splitting event continues until it can no longer be split or ends because of specific rules.

If you are using Scikit-Learn, you can control the hyperparameters, including the min samples leaf.

Officially, the min samples leaf parameter is “the minimum number of samples required to be at a leaf node.”

This means the split point at any depth will only be considered if it leaves at least min samples leaf training samples in each left and right branch.

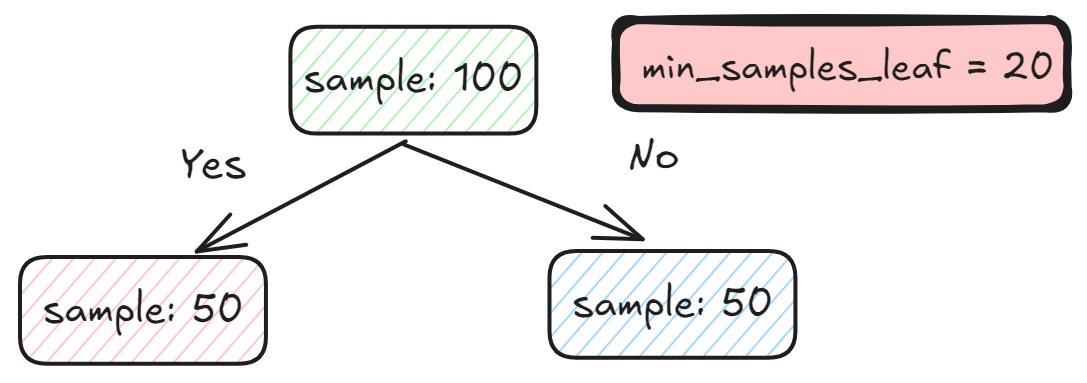
For example, below is a tree split from 100 samples to 50 samples for each branch. We also set the minimum sample leaf to 20.

The split is allowed as each sample on both the left and right sides is 50 (which is more than 20).

Let’s see if we change the split number to 90 and 10.

It didn’t work, and the split would stop where the terminal node would stop at the sample 100 leaf.

It’s cool that it can be stopped early, but what are the advantages of setting up the minimum sample leaf hyperparameter?

• A smaller value means the Decision Tree can grow deeper, leading to a more complex tree with potentially more splits—which can capture data-specific patterns, increasing the risk of overfitting.

• In contrast, higher values force the tree to be more restrictive and broader, which leads to more generalized decisions and simpler models. This could decrease the risk of overfitting but can also lead to underfitting.

Let’s take a look at the different decision boundaries of the decision tree model with different min samples leaf.

As we can see, the min samples leaf 1 has a very specific decision boundary where it would follow the data patterns.

With the increase of the min samples leaf, the decision boundary becomes clearer and totally separates at the higher min samples leaf value.

Generalization also comes with a much more preferable model performance. As we can see, increasing the min samples leaf parameter would increase the accuracy.

But would it always happen like that?

Let’s see if we keep increasing the min samples leaf effect to the accuracy.

Apparently, the accuracy only increases until a certain peak, then decreases after passing that point.

The model becomes much simpler and runs into an underfitting case.

Of course, many things affect accuracy, such as data pattern, dimension, algorithm complexity, etc.

However, there will always be a peak before the performance decreases, so finding the optimal number of minimum sample leaves becomes important.

---

FREE Learning Material for you❤️

👉Decision-Tree Model Building Metrics Explained in Detail

👉Decision Tree by the University of Pennsylvania

👉Data Science Learning Material

---

That’s all for today! I hope this helps you understand how min samples leaf can affect your model complexity and, subsequently, the model performance.

Any hyperparameters you think are much more important? Let’s discuss it together!

👇👇👇